
Typhoon is the most often extreme weather on earth and gives a massive threat to the safety of wind-sensitive structures, such as tall buildings, long-span bridges and other unique buildings 1. Compared with the traditional typhoon simulation method, the improved typhoon simulation method has higher accuracy in predicting the typhoon extreme wind speed in Hong Kong, increasing by about 8% and 11% respectively at 200 m height and gradient height. The results show that the improved typhoon simulation method can generate the correlations among all typhoon key parameters satisfactorily. The results show that the correlation coefficients among typhoon key parameters can be maintained satisfactorily with this improved typhoon simulation method. To validate this method, two aspects of analysis is carried out, including correlation analysis among typhoon key parameters and prediction of extreme wind speeds under various return periods. Then, this method is applied to the prediction of extreme wind speeds under various return periods in Hong Kong. In this paper, the improved typhoon simulation method is first given a detailed introduction. Issue: Not really a Latin hypercube.In order to further improve the prediction accuracy of typhoon simulation method for extreme wind speed in typhoon prone areas, an improved typhoon simulation method is proposed by introducing the Latin hypercube sampling method into the traditional typhoon simulation method.

This will "spread-out" the original data points, but will stay more true to the original data. Instead of a 20x20 histogram of the original data, create a 10x10 histogram of the original data and then take that forward to the final Monte Carlo sample (sample a grid cell, then sample inside the grid cell).Issue: If you believe that the other parts of the 2D space are valid, but didn't show up in the original sample, you might want to sample from more than the simple data locations. Instead of fitting the bivariate normal distribution, just bootstrap sample the original 200 data points in the last Monte Carlo simulation.Issue: loss of the original covariance structure
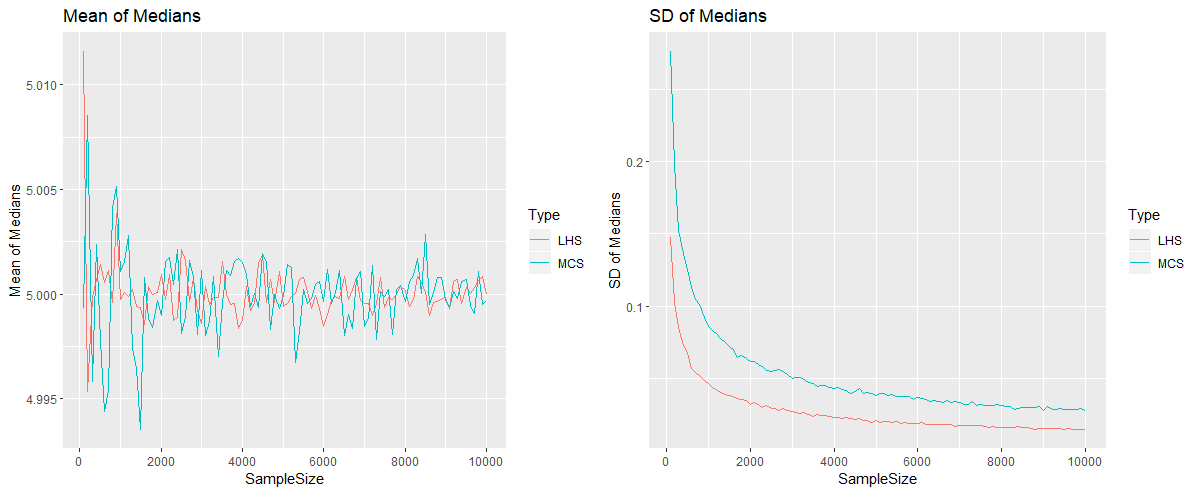
Instead of fitting the bivariate normal, fit two univariate normals to the margins and use those to transform the Latin hypercube.Continue with another Monte Carlo simulation.Sample from the bivariate normal with a Latin hypercube sample.Fit a bivariate normal distribution to the data.Is LHS using GPytorch feasible or is there some other solution that I should be exploring? I can probably do some hacky gradient descent to fit the $\frac$ sized areas but before I go down that route I thought I'd ask here for some help. However, the crux for me is that has no CDF implementation, and as far as I am aware the Multivariate Normal also has no inverse CDF. Ideally, I would like to sample this using Latin Hypercube Sampling as the output of this is the input to another Monte-Carlo simulation. (where pts are the white dots on the image above, larger = more samples at that point) Ind = np.random.choice(np.arange(mean_pred_np.size), p = p,size=1000) P = (mean_pred_np+np.abs(mean_pred_np.min())) In order to "sample" a position from the GP, I do the following: predictions = likelihood(model(test_x)) If I were to use the "true" histogram to sample points, it would be contained to the few cells with values which is why I've used a GP. Super(GPModelWithDerivatives, self)._init_(train_x, train_y, likelihood) From this, I generate a $20\times 20$ histogram and fit the fairly basic model class GPModel():ĭef _init_(self, train_x, train_y, likelihood): I have a small set ( $n \approx 200$ ) $(x,y)$ data points representing the find location of a person on a landscape.


 0 kommentar(er)
0 kommentar(er)
